Pourquoi échantillonner ?

Les questions abordées en écologie ou en étude de la biodiversité peuvent nécessiter d’observer voire de capturer des individus, pour les compter, les mesurer ou les peser ou encore pour déterminer leur sexe afin de calculer le sexe-ratio d’une population. Dans d’autres cas, le relevé de simples indices tels que des fèces, des poils, des traces d’ADN, des cris ou des chants, des nids ou terriers, peut suffire. C’est le cas, par exemple, lorsqu’on s’intéresse simplement à la présence d’une espèce dans une zone d’étude donnée.

Dans ces études en écologie, nous cherchons souvent à étudier des phénomènes qui interviennent à des échelles spatiales et temporelles relativement larges. Par exemple, nous pouvons chercher à savoir combien d’espèces d’oiseaux sont présentes dans une forêt donnée ; déterminer quelle est la taille des poissons dans un lac ou la densité d’individus d’une plante dans un parc national. Pour obtenir ces informations, il est souvent inconcevable d’être exhaustif : il serait impossible de parcourir toute la forêt pour espérer observer toutes les espèces présentes, de capturer tous les poissons du lac pour obtenir leur taille ou de parcourir toute la surface du parc national pour compter tous les individus de cette plante.

Dans une telle situation, il est nécessaire d’échantillonner. Échantillonner consiste à sélectionner un ensemble de petites sous-unités sur lesquelles les mesures de la variable d’intérêt seront effectuées. Les valeurs obtenues sur cet échantillon sont alors utilisées pour réaliser une inférence sur l’ensemble qui nous intéresse initialement. Cette démarche s’appelle l’échantillonnage. Les sous-unités sur lesquelles les mesures sont réalisées se nomment « individus statistiques ». L’ensemble de ces petites sous-unités mesurées se nomme « l’échantillon ». L’ensemble de toutes les petites sous-unités possibles dans la zone d’intérêt se nomme la « population statistique ». Dans les trois exemples précédents, on réaliserait par exemple des points d’écoute dans la forêt pour compter le nombre d’espèces d’oiseaux ; on capturerait un certain nombre de poissons pour mesurer leur taille et on compterait le nombre d’individus de la plante d’intérêt sur des quadrats dans le parc. Les valeurs obtenues sur ces échantillons d’individus statistiques seraient alors moyennées et ces moyennes seraient extrapolées à l’ensemble de la population statistique d’intérêt.

L’échantillonnage se justifie lorsque le phénomène qui nous intéresse est hétérogène dans le temps et/ou dans l’espace. Par exemple, s’il y a partout dans le parc national une densité homogène de plantes, il suffit de mesurer un quadrat dans le parc pour obtenir cette densité. De même, si tous les poissons du lac présentent la même taille, il suffit d’en mesurer un pour avoir la réponse à notre question. Cependant, les phénomènes naturels présentent en général une forte hétérogénéité. Par exemple, la densité de plantes varie avec l’altitude, le type de sol, le type de végétation environnante, etc. Il est donc nécessaire de mesurer plusieurs quadrats dans le parc pour bien couvrir toute cette variabilité et obtenir une densité moyenne que l’on extrapolera à l’ensemble du parc. Cette densité moyenne s’appelle une estimation. Il ne s’agit pas de la valeur exacte de la densité dans la population, car elle est obtenue sur un échantillon de cette population. La démarche d’échantillonnage aura donc pour objectif que cette estimation se rapproche le plus possible de la vraie valeur de la population. Pour cela, l’échantillonnage doit être conduit en suivant un processus rigoureux. Cette démarche s’accompagne en effet du risque de fournir des réponses fausses ou peu pertinentes. Deux éléments sont à considérer dans cette démarche :

1. Combien d’individus statistiques mesurer pour fournir une valeur suffisamment précise pour être utile ?
2. Comment sélectionner les individus statistiques à mesurer pour extrapoler à l’ensemble de la population statistique sans risque de fournir une valeur inexacte ?

Combien d’individus statistiques échantillonner ?

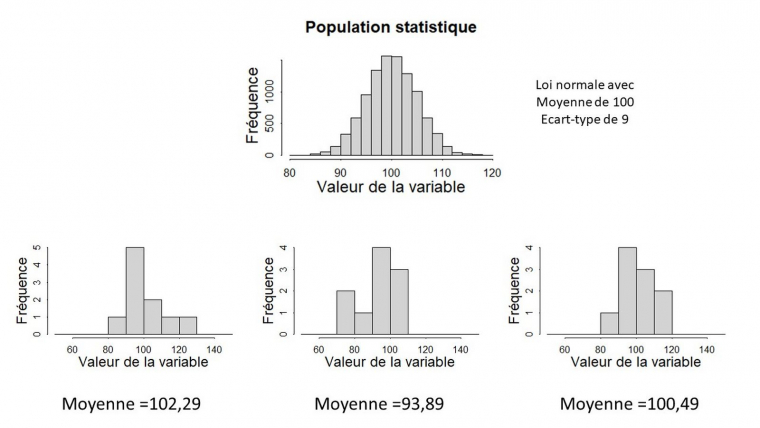
Commençons par examiner combien d’individus statistiques il convient de mesurer pour obtenir une estimation qui a du sens. Pour illustrer ce propos, restons sur notre exemple de la densité de plantes dans un parc national. Trois botanistes souhaitent obtenir cette densité. Ils réalisent pour cela des comptages sur de grands quadrats d’un hectare au sein du parc. À ce stade, considérons que ces quadrats sont sélectionnés au hasard dans le parc. La figure 1 ci-dessous présente les trois échantillons de trente quadrats qui ont été obtenus par chacun des botanistes. Le haut de la figure présente la vraie distribution de tous les quadrats possibles du parc. La moyenne de la population est de 100 individus par hectare. Le calcul de la moyenne de chacun des trois échantillons renvoie des valeurs sensiblement différentes et aucune ne renvoie la vraie moyenne de la population. Ce résultat est attendu du fait de l’hétérogénéité de la densité dans la population. Chaque tirage aléatoire conduit à un échantillon différent dont la moyenne diffère de la vraie moyenne de la population.

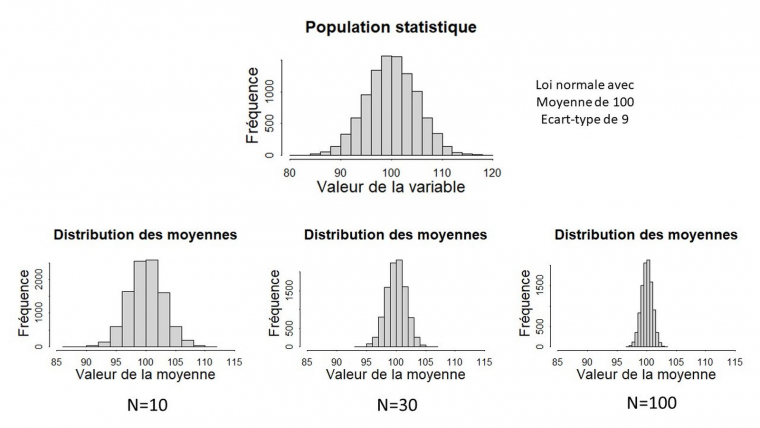
Pour mieux appréhender cette notion d’incertitude liée à l’échantillonnage, nous pouvons examiner comment varient les moyennes d’échantillons en fonction de leur taille. La figure 2 ci-dessous illustre ces relations. La vraie distribution de la population est représentée dans la moitié haute de la figure. La partie basse, quant à elle, présente la distribution des moyennes de 10 000 échantillons différents dont les individus ont été tirés aléatoirement dans la population et cela pour trois tailles d’échantillon différentes. Par cet exemple empirique, on constate que la distribution des moyennes, est centrée sur la vraie moyenne de la population. Ceci signifie que l’échantillonnage fournit ici une estimation qui n’est pas biaisée (en moyenne elle ne s’écarte pas systématiquement de la vraie moyenne). Nous verrons plus loin que cette propriété très importante dépend de la manière dont les individus statistiques ont été sélectionnés. L’autre élément à retenir de cette figure est que plus la taille de l’échantillon augmente, plus la distribution des moyennes est resserrée autour de la vraie moyenne de la population. Autrement dit, plus la taille de l’échantillon augmente, plus on a de chances que la moyenne obtenue sur un échantillon soit proche de la vraie valeur recherchée.

Plus les échantillons sont de taille importante, moins il est probable que la moyenne estimée sur cet échantillon soit éloignée de la vraie valeur de la population. On est donc plus confiant dans les moyennes estimées sur un grand échantillon que sur un petit. Cette propriété de l’échantillonnage est formalisée par un théorème qui fonde toutes les statistiques : le théorème central limite. Ce théorème formule plusieurs constats sur la distribution des moyennes issues d’échantillons. Le plus important pour nous ici étant que l’écart-type de la distribution des moyennes, que l’on nomme erreur standard, est égal au ratio entre l’écart-type de la distribution de la population (noté $\sigma$) et la racine carrée de la taille de l’échantillon noté $N$ (Équation $\eqref{erreurstandard}$).

$$\begin{equation} \text{Erreur standard} = \dfrac{\sigma}{\sqrt{N}} \label{erreurstandard} \end{equation}$$

Cette erreur standard est donc une information sur la précision de l’estimation. Elle peut être utilisée pour calculer un intervalle de confiance de la moyenne, à un seuil de confiance choisi, par exemple 95 %, à partir d’un échantillon. Cet intervalle s’interprète ici comme le fait qu’il y ait 95 % de chance que la vraie moyenne de la population soit comprise dans cet intervalle. Par exemple, pour nos plantes, on obtiendra avec le premier échantillon de la figure 1 une moyenne de 102,29 individus par quadrat (somme des comptages divisée par le nombre de quadrat comptés) et un intervalle de confiance à 95 % de [95,25 – 109,33]. Dans le cas de données qui suivent une loi normale, cet intervalle se calcule avec la moyenne à laquelle on ajoute ou retranche 1,96 fois l’erreur standard. Cette erreur standard est fournie en divisant l’écart-type (racine carrée de la somme des carrés des écarts entre chaque comptage et la moyenne) par la racine carrée du nombre de quadrats comptés (voir Équation $\eqref{erreurstandard}$).

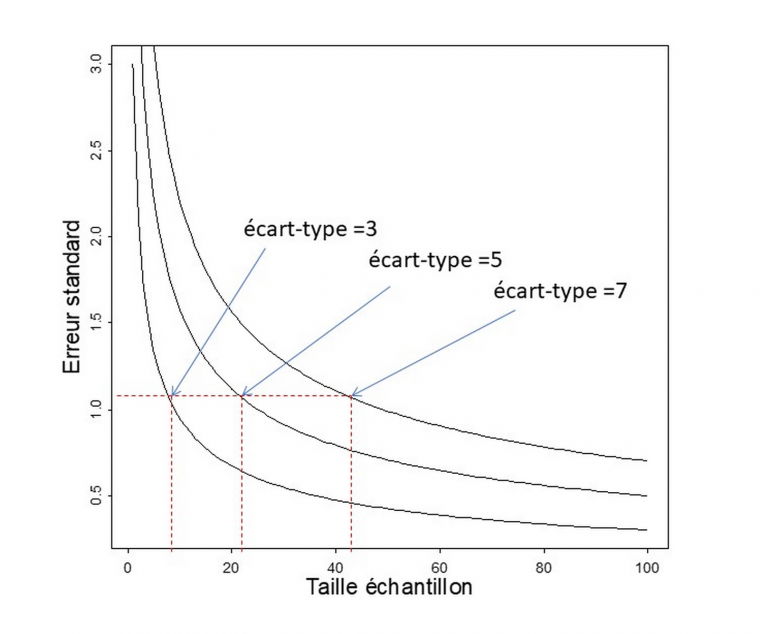
Le théorème central limite indique donc qu’un échantillon fournira une estimation d’autant plus précise que sa taille sera grande. Ceci peut rapidement conduire à conseiller de mesurer le plus d’individus statistiques possibles. Cependant deux éléments s’opposent à ce conseil très général. D’une part le budget pour un travail de terrain est souvent contraint par le financement disponible. Cette contrainte conditionne, de fait, la taille de l’échantillon mesurable sur le terrain. La question qui se posera dans ce cas est : est-ce que ma taille d’échantillon sera suffisante pour tirer des conclusions utilisables ? En termes plus statistiques on dira : est-ce que ma taille d’échantillon est suffisante pour que la précision de mes estimations me permette de tirer des conclusions interprétables ? D’autre part, la précision d’une estimation n’évolue pas de manière linéaire avec la taille de l’échantillon. En effet pour une population donnée, la relation entre la taille de l’échantillon et cette précision suit une exponentielle négative (Figure 3). Ceci est lié au fait que la taille de l’échantillon est au dénominateur et associée à une racine carrée dans le théorème central limite. L’ajout d’un individu statistique à un échantillon de petite taille conduira à une plus forte amélioration de la précision d’une estimation que l’ajout d’un individu à un échantillon déjà de grande taille. Il y a donc un compromis à trouver entre taille d’échantillon et précision minimum souhaitée. Une plus grande taille d’échantillon fournira toujours une estimation plus précise mais le gain en précision pourra être limité, voire très limité. Dans cette situation le budget investi dans ces mesures supplémentaires pourrait être avantageusement investi ailleurs. Au contraire, l’ajout d’un individu statistique supplémentaire à un échantillon de petite taille peut faire une grosse différence en termes de précision et la recherche d’un budget supplémentaire pour mesurer un ou quelques individus en plus peut s’avérer très importante pour pouvoir tirer des conclusions d’une étude dans ce cas.

Il est important de noter que la formule présentée ci-dessus (Équation $\eqref{erreurstandard}$) fait aussi intervenir l’écart-type de la distribution de la variable étudiée dans la population cible et cela en numérateur. Cela a pour conséquence que pour une même taille d’échantillon, une estimation sera moins précise dans une population hétérogène sur la variable mesurée que dans une population homogène.

Le fait de disposer de cette formule présente un intérêt considérable : on peut anticiper, lors de la construction d’une étude, la précision que l’on obtiendra sachant le budget disponible ou anticiper le budget nécessaire pour obtenir un degré de précision préalablement déterminé. Il faut pour cela cependant disposer de quelques informations, notamment de l’écart-type et de la moyenne de la distribution de la variable. Ces valeurs peuvent être obtenues par une étude préliminaire. Il s’agit de mener une étude sur le terrain dans les mêmes conditions que l’étude prévue (même protocole de mesure, même population étudiée, etc.) mais avec un effort d’échantillonnage limité. Cet échantillonnage permettra, s’il n’est pas trop petit, de fournir une première estimation de la moyenne et de l’écart-type de la variable étudiée dans la population cible. Ces valeurs pourront alors être mobilisées pour anticiper sur l’échantillonnage à conduire ultérieurement et sur sa précision attendue. Lorsqu’une étude préliminaire n’est pas possible, des valeurs approximatives de moyenne et d’écart-type peuvent être extraites de la littérature scientifique ou à dire d’expert.

Quels individus statistiques échantillonner ?

L’objectif d’un échantillonnage et des analyses statistiques réalisées sur les données de cet échantillon est de pouvoir extrapoler les estimations obtenues sur l’échantillon à l’ensemble de la population statistique d’intérêt. On parle aussi d’inférence statistique. Ceci suppose une définition précise de cette population statistique au risque de ne pas savoir exactement à quoi on cherche à extrapoler et au risque de construire un plan d’échantillonnage qui ne répond pas à la question initiale. De fait, la définition de la population statistique doit être explicite dans la formulation de la question. Par exemple « quelle est la densité de pipits spioncelles dans le parc national du Mercantour ? » ne définit pas la même population statistique que « Quelle est la densité de pipits spioncelles dans les pelouses alpines du parc national du Mercantour ? ». Dans un cas la population statistique est l’ensemble de la surface couverte par le parc, incluant des pelouses occupées par l’espèce bien entendu, mais aussi des endroits totalement défavorables à l’espèce : forêts, zones urbanisées, etc. Dans l’autre cas, la population d’intérêt n’est constituée que des pelouses alpines. La réponse à ces deux questions fournira des résultats bien différents. L’échantillonnage sera en effet différent et la moyenne des densités obtenues sera bien plus élevée dans le second cas que dans le premier. Cette situation est un peu caricaturale, mais des situations plus ambiguës sont fréquentes et peuvent conduire à obtenir des estimations biaisées (ou à des résultats contradictoires entre études du fait de différences, parfois subtiles sur la définition de la population statistique).

Pourquoi est-il si important de définir la population statistique de manière explicite ? En fait, cela tient largement au fait qu’un échantillonnage rigoureux se doit de reposer sur une sélection aléatoire des individus statistiques au sein de cette population. Cette sélection aléatoire est une condition sine qua non pour permettre une extrapolation sans risque. En effet, la théorie de l’échantillonnage et notamment la théorie autour du théorème central limite repose sur l’hypothèse que tous les individus statistiques disposent de la même probabilité d’être sélectionnés dans l’échantillon. Assurer que tous les individus statistiques ont la même probabilité d’être sélectionnés dans l’échantillon, implique de pouvoir lister ces individus et donc de définir la population statistique. Dans les situations où les individus ont des probabilités inégales (et non connues) d’être sélectionnés, il n’est pas possible de se reposer sur le théorème central limite pour qualifier la précision des estimations. Il n’est pas non plus possible de certifier que les estimations ne sont pas biaisées. Un petit exemple peut facilement illustrer ce propos : dans le cadre d’une étude sur la densité du pipit spioncelle, les agents d’un parc national ont réalisé des points d’écoute sur des zones connues par un agent pour abriter l’espèce et accessibles grâce à un sentier. Les estimations de cet échantillon de points ne peuvent être extrapolées qu’à l’ensemble des zones connues pour abriter l’espèce, accessibles par un sentier et connues par cet agent. Rien ne garantit que les densités soient du même ordre dans les zones loin des sentiers ou dans les zones de pelouses alpines pour laquelle la présence de l’espèce n’est pas connue. On peut facilement imaginer qu’un expert de l’espèce adoptant la même stratégie à partir de ses propres connaissances obtiendrait des résultats radicalement différents.

Il existe de très nombreux types de plans d’échantillonnage, reposant tous sur une sélection aléatoire des individus statistiques, mais permettant de gérer des situations ou des questions différentes. Ce domaine est foisonnant et il n’est pas possible ici de lister tous ces plans. Nous présentons cependant les plans les plus fréquemment utilisés pour l’étude de la biodiversité.

Échantillonnage aléatoire simple

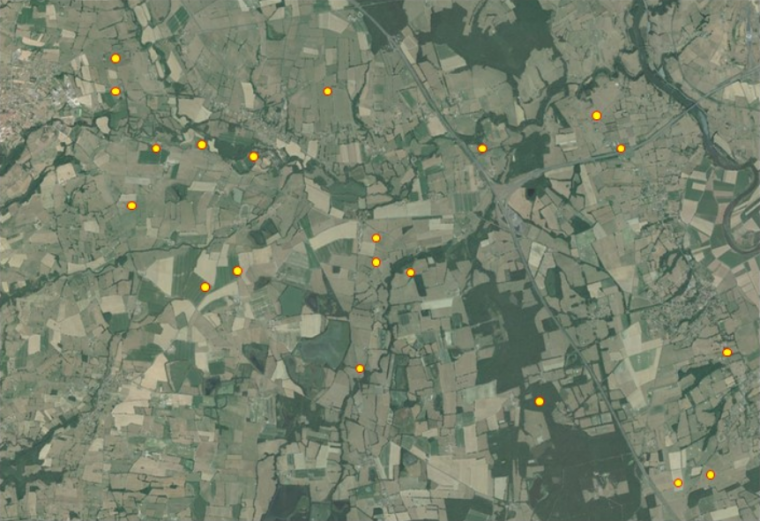
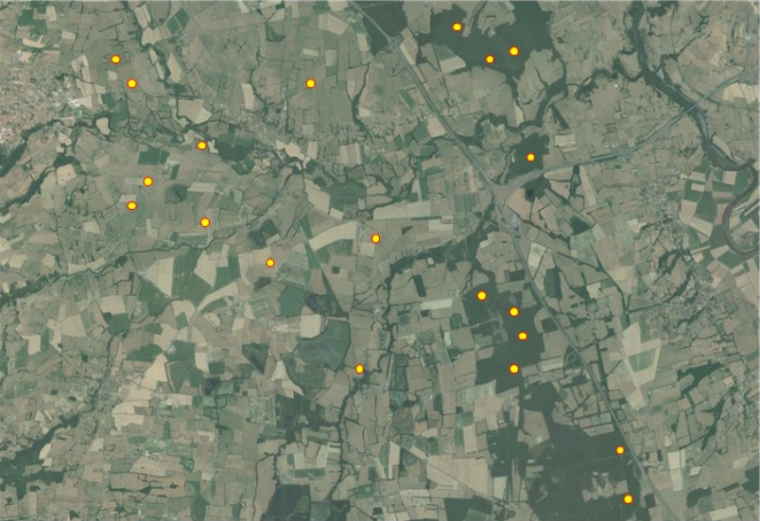
Le plan d’échantillonnage le plus courant est le plan d’échantillonnage aléatoire simple. Il consiste, à partir de la définition d’une liste d’individus statistiques (appelés aussi unités d’échantillonnage) composant la population statistique d’intérêt, à réaliser un simple tirage aléatoire sans remise au sein de cette liste d’unités (Figure 4). Ce tirage peut être en pratique réalisé avec un tableur ou avec un logiciel de programmation, comme R.

Le plan d’échantillonnage aléatoire simple est facile à mettre en œuvre et fournit des données très aisément analysables par des statistiques usuelles. Il présente cependant la limite de ne pas fournir les estimations les plus précises pour une taille d’échantillon donnée, en particulier quand la population statistique présente une forte variabilité de la variable étudiée. Par ailleurs, il conduit généralement à avoir des agrégats de points dans certaines zones et, au contraire, des zones vierges de points, ce qui peut limiter fortement le potentiel du dispositif à détecter des variations spatiales de la variable étudiée.

Échantillonnage aléatoire stratifié et pondéré

Lorsque l’observateur sait, ou suppose, que sa population statistique cible est très hétérogène sur la variable mesurée et connaît a priori les facteurs expliquant cette hétérogénéité, il a tout intérêt à exploiter cette connaissance lors de la construction de son échantillon. Le cas le plus fréquent en écologie est celui d’une variation spatiale de la variable mesurée. Il peut s’agir par exemple d’une hétérogénéité de densités d’une plante entre habitats ouverts et fermés, ou des variations de probabilités de floraison selon des tranches d’altitude, etc. Dans le cas d’un échantillonnage aléatoire simple, la forte variabilité au sein de la population conduira à une importante erreur standard associée à cette estimation. Dans cette situation, il est plus efficace d’échantillonner les différents sous-groupes identifiés au sein de la population statistique. Ces sous-groupes seront plus homogènes, l’estimation au sein de chaque sous-groupe sera relativement précise et leur combinaison sera plus précise que celle associée à un tirage aléatoire simple. Ces groupes sont appelés des strates dans le langage statistique, d’où le terme « échantillonnage aléatoire stratifié » (Figure 5). À noter qu’au sein de chaque strate, les individus statistiques doivent être sélectionnés aléatoirement.

Dans le cas d’un échantillonnage aléatoire stratifié, une des questions majeures qu’il faut aborder repose dans la répartition des individus de l’échantillon au sein de chaque strate. Cette question a fait l’objet de travaux assez pointus, analytiques, qui montrent d’une manière générale qu’il est préférable de ne pas répartir équitablement le nombre d’individus dans chaque strate.

En comparaison avec un plan d’échantillonnage aléatoire simple, un plan d’échantillonnage aléatoire stratifié ne présente que des avantages. Il ne résout cependant pas une des principales limites du plan d’échantillonnage aléatoire, à savoir une répartition des unités d’échantillonnage très déséquilibrée dans l’espace qui peut limiter l’exploitation au-delà de la simple estimation d’une moyenne.

Plan d’échantillonnage systématique

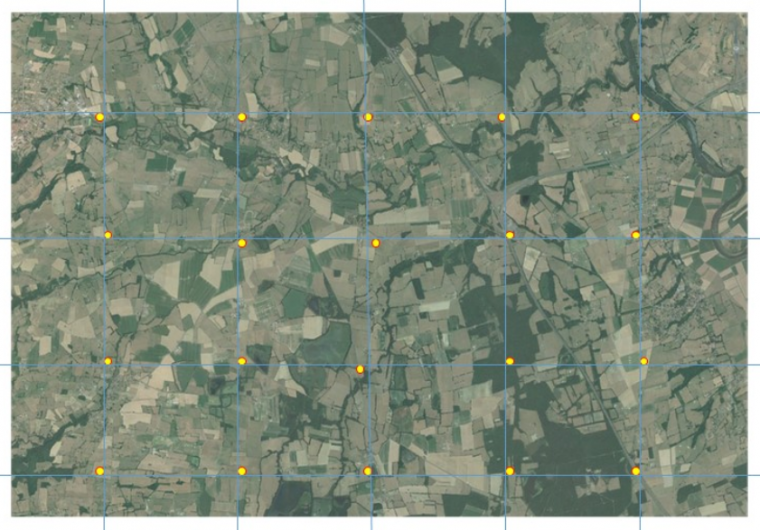
Une autre solution pour échantillonner une population statistique repose sur la répartition homogène des unités d’échantillonnage dans l’espace. En pratique, cela consiste à caler une grille sur la zone d’étude pour placer les unités d’échantillonnage à des distances égales tout en couvrant l’ensemble de la zone. Ce type de plan est appelé plan d’échantillonnage systématique et est particulièrement adapté dès lorsqu’il existe des gradients spatiaux de la variable étudiée au sein de la zone d’étude (Figure 6). L’existence de tels gradients est fréquente (gradients latitudinaux, distance à la mer, altitude…). Ce type de plan permet de répartir des unités d’échantillonnage le long du gradient spatial et par conséquent de pouvoir efficacement le mettre en évidence.

Ce type de plan peut sembler peu aléatoire sur le principe. Pourtant, dès lors que la grille est placée au hasard sur la zone, chaque individu statistique de la population statistique a exactement la même probabilité d’être sélectionné par le plan, ce qui confirme bien le côté aléatoire de ce type de plan.

Ce type de plan résout donc un des défauts majeurs des plans présentés précédemment à savoir le déséquilibre dans la répartition spatiale des unités d’échantillonnage. Cependant, tout comme le plan aléatoire simple, il ne sera pas optimal s’il existe des strates bien différentes au sein de la population statistique. Par ailleurs, il peut poser certaines difficultés logistiques notamment dans des zones à fort relief. Un tel plan en montagne par exemple, conduira à devoir passer d’une vallée à une autre, à franchir une crête, etc. rendant les temps de déplacements entre les unités très importants et, de fait, le dispositif assez inefficace.

Plan d’échantillonnage à plusieurs niveaux

Tous les plans proposés ci-dessus présentent des avantages et des inconvénients. S’ils ont été longtemps la palette disponible en écologie, de nombreux travaux de statisticiens ont consisté à développer des plans plus complexes adaptés à des situations plus ou moins générales. Un des axes de développement des plans d’échantillonnage repose sur l’emboîtement de plusieurs niveaux d’échantillonnage. Par exemple, on échantillonne des parcelles au sein d’une population de parcelles (premier niveau) puis des quadrats au sein des parcelles sélectionnées (deuxième niveau). Ce type de plan a encore peu été utilisé en écologie, mais a été très largement utilisé dans des dispositifs plus expérimentaux en agronomie. Une des difficultés associées à ces plans réside dans l’analyse des données collectées du fait qu’il existe différents niveaux de variabilité dans ces données (variabilité interquadrat, intraparcelle, variabilité interparcelle par exemple) et oblige à utiliser des méthodes d’analyses des données pointues.

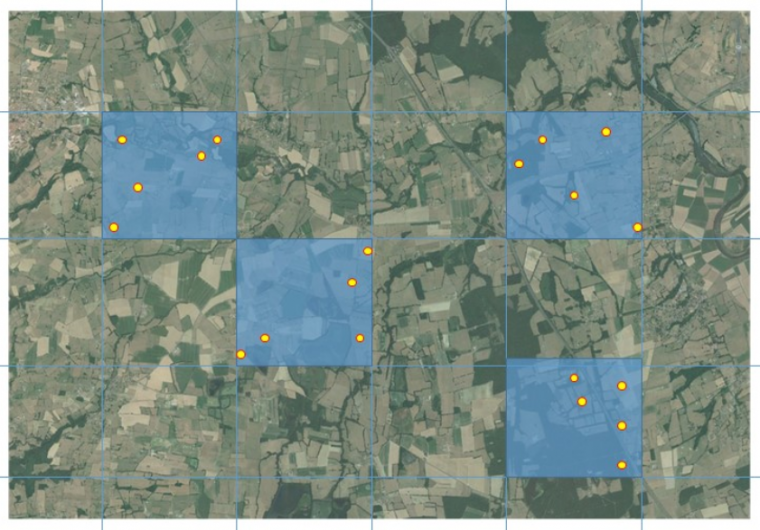
La figure 7 présente un plan d’échantillonnage pour mesurer des densités de vers de terre dans des sols. Il repose sur deux niveaux d’échantillonnage : des mailles et des points au sein des mailles. Une grille est posée sur la zone d’étude définissant des unités d’échantillonnage de grande taille. On réalise un tirage aléatoire de mailles au sein de cette grille, le nombre de maille tiré correspond au nombre de matinées disponibles pour réaliser les mesures sur le terrain. Au sein de chaque maille, un tirage aléatoire est réalisé pour déterminer la localisation des cinq points sur lesquels seront effectués les prélèvements de vers de terre. Les unités d’échantillonnage sont de fait les points de prélèvements, la population statistique l’ensemble des points de la zone d’étude. La sélection des points de prélèvements étant basé sur un (même deux) tirage(s) aléatoire(s), les données peuvent être analysées avec des statistiques inférentielles. Ce plan présente deux avantages : (i) d’un point de vue pratique, le fait de sélectionner un ensemble de points au sein d’une même maille assure de ne pas perdre trop de temps en déplacements et de pouvoir échantillonner plusieurs points au sein d’une même matinée, (ii) l’emboîtement des échelles spatiales permet d’estimer la variabilité intramaille et la variabilité intermaille, ce qui peut être intéressant pour comprendre comment se structure la variable d’intérêt dans l’espace.