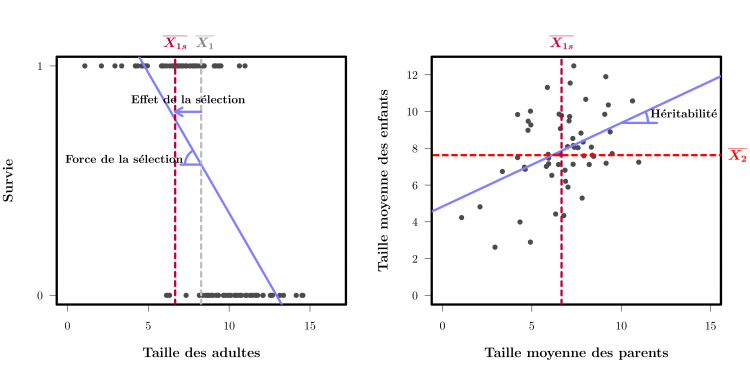
Ces deux graphiques développent l’approche de génétique quantitative présentée Figure 1. Le graphique à gauche montre comment une régression linéaire permet de mesurer la pression de sélection agissant sur la taille. Chaque point représente un individu, avec sa taille en abscisses et la survie jusqu’à l’âge de reproduction en ordonnées (0 pour mort avant de pouvoir se reproduire, 1 pour survie). La pente de la régression est une mesure objective de la force de la sélection. L’effet de la sélection, c’est à dire le changement de taille moyenne après sélection, peut-être obtenu en multipliant cette pente par la variance en taille et en divisant par la survie moyenne (ce qui est équivalent à la covariance entre la taille et la survie, divisé par la survie moyenne). Pour simplifier, on ne représente ici que la sélection due à la viabilité, et on ignore la sélection liée à la reproduction.
Sur le graphique de droite chaque point correspond à la taille moyenne des enfants d’un couple (en ordonnées) en fonction de la taille moyenne de leurs deux parents (en abscisses) montre comment la régression linéaire peut aussi être utilisée pour mesurer l’héritabilité, c’est-à-dire la proportion de variation d’un caractère qui est due aux gènes. La pente entre la taille moyenne des parents et la taille moyenne des enfants reflète la transmission de gènes ayant un effet sur la taille ; plus la pente est forte, plus les gènes expliquent une part importante de la variation en taille. En multipliant l’effet de la sélection par l’héritabilité, on peut prédire le changement génétique entre les deux générations.
Ces deux techniques sont facilement généralisables pour mesure la sélection qui agit via la fécondité plutôt que la survie, pour mesurer la sélection agissant sur plusieurs traits simultanément, pour corriger pour les sources de similarités non-génétiques entre apparentés, ou encore pour estimer le rythme de changement génétique sur plusieurs générations...