Explication de la différence entre les termes d'échelle, de grossissement et d'agrandissement. Méthode de calcul de ces différentes valeurs.
Situation du problème : « Qu’est-ce que cela veut dire ? Qu’est-ce qu’il faut faire ? »
L’enseignement des sciences de la vie implique de nombreux travaux pratiques. Parmi ceux-ci, les observations d’échantillons macroscopiques, à l’œil nu ou à la loupe binoculaire, et de coupes microscopiques amènent souvent à demander aux élèves de réaliser un dessin représentant ce qu’ils ont pu observer.
La réalisation de tels dessins d’observation pose le problème du rapport entre le dessin réalisé et la taille réelle de l’objet observé. Un travail rigoureux ne peut s’envisager sans une mention permettant de visualiser ce rapport de taille, ou au minimum une mention indiquant le degré de précision de l’observation.
Dans cette optique, on retrouve souvent employés les termes « échelle », « grossissement », « agrandissement », « grandissement ». Or ces termes sont souvent confondus, et utilisés de manière indifférente, alors qu’ils ont en fait des significations extrêmement différentes. Ceci peut engendrer (aussi bien chez les enseignants que chez les élèves) une confusion malheureuse qui peut mener dans certains cas à des erreurs de compréhension.
Ce document se propose donc, dans un premier temps, de reprendre les définitions de ces termes en les illustrant et en expliquant leurs utilités relatives. Dans un deuxième temps sont proposées quelques techniques pour l’utilisation concrète de ces termes lors d’une observation microscopique.
Des termes différents pour des utilisations différentes
Définitions
Agrandissement (ou grandissement)
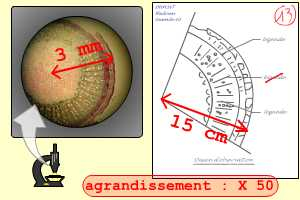
Une coupe de tige de rayon 3 millimètres est dessinée sous la forme d’un dessin où cette tige fait 15 centimètres de rayon. Agrandissement : × 50.
L’agrandissement est le rapport entre la taille du dessin d’observation réalisé et la taille réelle de l’objet. Il est noté sous la forme « × n », avec n la valeur de ce rapport.
Échelle
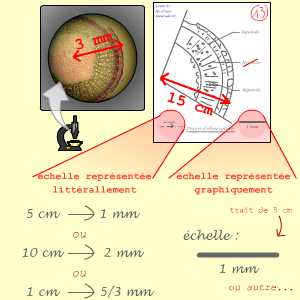
Une coupe de tige de rayon 3 millimètres est dessinée sous la forme d’un dessin où cette tige fait 15 centimètres de rayon.
L'échelle peut être notée 5 cm → 1 mm ou 10 cm → 2 mm ou 1 cm → 5/3 mm, etc. ou sous la forme d'une représentation graphique.
L’échelle est une indication de la correspondance entre la taille du dessin et la taille réelle de l’objet. L’échelle est donc une manière différente de noter l’agrandissement. On peut représenter une échelle de deux manières :
- littérale : « Y cm → Z mm » (avec Y une longueur sur le dessin, Z la longueur réelle correspondante) ;
- graphique : une barre présente sur le dessin indique une taille précisée.
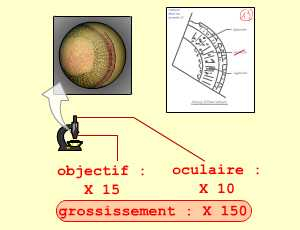
Une préparation microscopique est observée à l’aide d’un microscope possédant un oculaire × 10 et sous l’objectif × 15. Ceci permet d’observer un niveau de détail suffisant à la réalisation du dessin.
Grossissement : × 150
Grossissement
Le grossissement indique le grossissement de l’appareil optique (microscope ou loupe) qui a permis de réaliser l’observation et donc le dessin. Il est obtenu en multipliant les grossissements des éléments de l’appareil optique (objectif, oculaire, etc.). Il est noté sous la forme « × n », avec n le grossissement utilisé.
Utilisation pratique
Les exemples présentés ci-dessus démontrent bien la nécessité de ne pas confondre les termes de grossissement et d’agrandissement (ou d’échelle) : pour un dessin final identique, on peut parfaitement faire figurer l’agrandissement (× 50 ici) ou le grossissement utilisé (× 150). Or ces deux valeurs peuvent être très différentes et ne représentent pas la même chose. Ainsi, il est à noter que les échelles (donc les agrandissements) sont trop peu souvent indiqués dans les manuels scolaires ou les livres… Il est alors difficile pour le lecteur de connaître la taille réelle de l’objet représenté. Par souci de simplicité c’est souvent le grossissement utilisé qui est figuré, parfois en omettant de préciser qu’il s’agit d’un grossissement et non pas d’un agrandissement…
Il peut donc être judicieux pour les enseignants de SVT de présenter aux élèves quelques notions sur ces différents termes. Ceci devrait leur permettre de comprendre que, lorsqu’ils observent une photographie de cellule au microscope électronique à transmission agrémentée d’un joli « × 10 000 », cela ne signifie pas que l’image qu’ils voient a été agrandie 10 000 fois, mais seulement que le grossissement du microscope était de 10 000 lors de la prise de la photographie.
Concrètement, lors d’un travail d’observation, calculer puis représenter une échelle ou un agrandissement peuvent être légèrement complexes, et surtout prendre trop de temps (voir ci-dessous les « trucs et astuces » pour ces calculs). Ainsi, bien qu’il soit préférable d’indiquer l’agrandissement (car ceci a plus de valeur réelle), on peut en général se limiter à noter le grossissement utilisé. Toutefois, il convient alors de noter clairement le choix réalisé, en précisant « grossissement : × 50 » par exemple. En absence de précision, il est impossible de savoir si la valeur notée correspond à un agrandissement ou à un grossissement, et ceci n’a donc alors aucune valeur.
Trouver grossissement et agrandissement lors d’un travail au microscope
Le grossissement : une simple multiplication
B. Cet oculaire indique un grossissement de × 10.
C. Cet objectif indique un grossissement de × 2,5.
Une observation avec cet oculaire et cet objectif se réalise donc à un grossissement de : × 25 (10 × 2,5 = 25).
Le grossissement étant simplement le grossissement fournit par le microscope, il est obtenu en multipliant les grossissements individuels des différents éléments du microscope. Ceux-ci sont notés sur les éléments optiques. En général, on obtient donc le grossissement en multipliant le grossissement de l’oculaire par le grossissement de l’objectif.
Remarque : Il peut arriver d’avoir à prendre en compte les grossissements d’éléments optiques supplémentaires. C’est le cas par exemple de microscopes équipés d’un optovar sur l’oculaire. Ces équipements sont, en général, absents du matériel disponible dans les collèges et lycées.
L’agrandissement : proportionnalité et connaissance du matériel
L’agrandissement se trouve donc en divisant la dimension de l’objet dessiné (ou d’un élément de l’objet dessiné) par la dimension du même objet (ou du même élément) dans la réalité. Toute la difficulté est donc de connaître cette taille réelle. Pour ceci, deux techniques sont possibles en fonction du matériel disponible :
- Utilisation d’un micromètre oculaire. C’est bien évidemment la méthode de choix lorsque l’on dispose de cet équipement.
- De manière générale, un collège ou un lycée ne dispose pas de micromètre oculaire (ou bien en nombre insuffisant). On peut alors déterminer une taille approximative réelle grâce à diverses méthodes.
Comment procéder en l’absence de micromètre oculaire ?
Le plus simple dans ce cas est de déterminer la dimension du champ oculaire, c’est-à-dire le diamètre du champ que l’on peut voir en regardant dans le microscope. L’intérêt est ici qu’une fois cette dimension déterminée aux différents grossissements utilisés, on peut la réemployer lors de toutes les utilisations ultérieures du microscope. On peut d’ailleurs envisager en classe de donner cette valeur aux élèves au lieu de la leur faire calculer (gain de temps certain, mais perte d’un intérêt pédagogique net…). Attention ! Cette dimension du champ oculaire doit être déterminée pour chaque microscope, en particulier s’il s’agit de modèles différents !
Pour déterminer la dimension du champ oculaire, en l’absence de micromètre oculaire, la solution la plus simple est de le faire à faible grossissement. Pour cela, il suffit de placer sous le microscope une règle transparente en plastique ou du papier millimétré (avec un bon éclairage, on voit très bien « à travers », et donc la graduation). Voir exemple ci-après.
Cette méthode, si elle reste extrêmement simple, n’est malheureusement pas utilisable à un grossissement même moyen et encore moins au fort grossissement. Pour connaître la dimension du champ oculaire à ces grossissements on interpole donc à partir de la dimension du champ à faible grossissement, en supposant une réelle proportionnalité entre ces valeurs (voir exemple ci-après). On peut noter que cette méthode n’est pas très rigoureuse, des variations existant entre les différents grossissements les objectifs n’étant pas les mêmes. Elle reste toutefois suffisante au niveau collège-lycée.
Exemple de calcul d’agrandissement
Étape 1 : détermination du diamètre du champ oculaire à faible grossissement
A. Vue d’une règle transparente graduée tous les 0,5 millimètres au faible grossissement.
B. Vue d’un papier millimétré au faible grossissement. Chaque carré fait 0,5 millimètres de côté.
À faible grossissement (oculaire × 12,5, objectif × 6,3), on observe une règle transparente (à gauche) ou un morceau de papier millimétré (à droite).
Ici, notre champ oculaire fait dont un diamètre de 2,5 mm. Il ne s’agit bien entendu que d’une mesure approximative.
Étape 2 : interpolation aux autres grossissements
Sur ce microscope, nous disposons de trois objectifs. Nous pouvons donc maintenant proposer une valeur approchée du diamètre du champ à ces trois grossissements :
| Grossissement oculaire | Grossissement objectif | Grossissement total | Diamètre champ oculaire | |
|---|---|---|---|---|
| Faible grossissement | 12,5 | 6,3 | 12,5 × 6,3 = × 75,6 |
2,5 mm |
| Moyen grossissement | 12,5 | 25 | 12,5 × 25 = × 312,5 |
2,5 × 75,6 / 312,5 = 0,6 mm |
| Fort grossissement | 12,5 | 40 | 12,5 × 40 = × 500 |
2,5 × 75,6 / 500 = 0,38 mm |
Attention : Ces valeurs ne sont valables que sur notre seul microscope ! Elles doivent être déterminées de manière indépendante pour chaque microscope.
Étape 3 : mesure sur le dessin
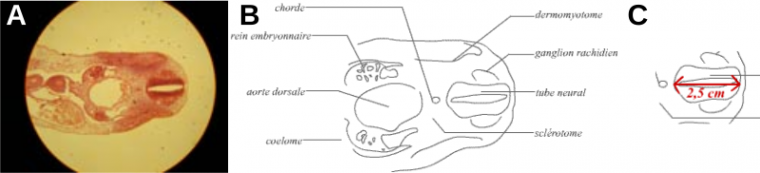
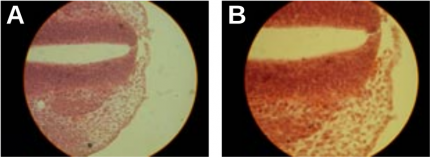
Nous utilisons ici une coupe transversale d’embryon de lapin de 12 jours. Ceci nous permet d’observer le tube neural de cet embryon. Il nous est donc possible de le dessiner.
A. Observation à faible grossissement (× 75,6).
B et C. Sur le dessin réalisé, le tube neural mesure 2,5 cm (selon l’axe dorso-ventral).
Étape 4 : calcul du rapport de l’agrandissement
Pour calculer l’agrandissement réalisé lors de notre dessin, il ne nous reste donc plus qu’à connaître la taille réelle de ce tube neural. Or, il nous apparaît ici que le tube neural n’occupe qu’une partie du champ oculaire lors de notre observation à faible grossissement : il est difficile de dire s’il représente un cinquième du diamètre du champ oculaire, ou bien un sixième, ou encore une autre valeur.
A. Observation à moyen grossissement (× 312,5)
B. Observation à fort grossissement (× 500)
Il est possible ici de passer au moyen ou au fort grossissement. On s’aperçoit, en déplaçant la préparation sous l’objectif pour mieux l’observer que le tube neural occupe environ les deux tiers du diamètre du champ à moyen grossissement, ou environ tout le diamètre à fort grossissement. Ceci correspondrait donc à une taille de 0,4 mm (2/3 × 0,6 mm à moyen grossissement) à 0,38 mm (diamètre du champ à fort grossissement). On peut donc proposer une taille approximative de 0,4 mm pour ce tube neural. (On peut noter que ceci correspond bien à l’impression que l’on avait à faible grossissement : 1/6 × 2,5 = 0,41 mm)
En conclusion ici, on peut achever de déterminer l’agrandissement de notre dessin :
- représentation de 25 mm pour une taille réelle de 0,4 mm.
- 25 / 0,4 = 62,5
- Agrandissement : × 62,5
On pourrait admettre un agrandissement approximatif de 60 fois étant donné les imprécisions de cette méthode.
Bien entendu, il n’est pas toujours nécessaire de passer à un fort grossissement. Tout dépend de la préparation étudiée. Dans l’idéal, on cherche aussi à mieux centrer la préparation que dans ces photographies.